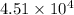Answer:
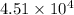
Step-by-step explanation:
We are given that
Thickness of glass plate=3.45 mm=
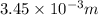
Using
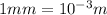
Refractive index=
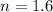
Wavelength in air,
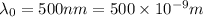
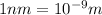
Distance from source to screen=d=2.05 cm=
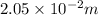
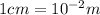
Wavelength in medium=
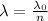
Using the formula
Wavelength in medium=
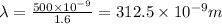
Distance between source and scree except glass plate=
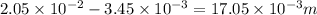
Number of wavelength=
![(distance];in\;air)/(wavelength\;in\;air)+(distance\;in\;glass)/(wavelength\;in\;glass)](https://img.qammunity.org/2021/formulas/physics/college/m0aopn230pr6gltxnzykuazc50gsxe3fu7.png)
Number of wavelength=
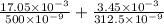
Number of wavelength=