Rectangle ABCD has vertices at A (-1, 1), B (2, 1), C (2, -5), and D (-1, -5). What is the perimeter of rectangle ABCD?

Question

asked Dec 7, 2021 146k views

2 Answers

Rick Mac Gillis · Answer 1 · 2021-12-11T19:17:13+0000

Solution:

The perimeter of rectangle is:

Perimeter = 2( length + width)

Rectangle ABCD has vertices at A (-1, 1), B (2, 1), C (2, -5), and D (-1, -5)

Let AB be the length

Let BC be the width

Find distance between A and B

The distance between two points is given as:

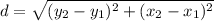
d = √((y_2-y_1)^2+(x_2-x_1)^2)

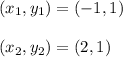
$(x_1, y_1) = (-1, 1)\\\\(x_2, y_2) = (2, 1)$

Therefore,

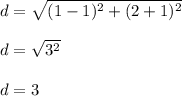
$d = √((1-1)^2+(2+1)^2)\\\\d = √(3^2)\\\\d = 3$

Thus, AB = length = 3 units

Find the distance between B and C

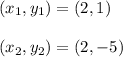
$(x_1, y_1) = (2, 1)\\\\(x_2, y_2) = (2, -5)$

Therefore,

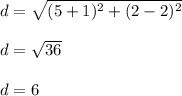
$d = √((5+1)^2+(2-2)^2)\\\\d = √(36)\\\\d = 6$

Thus width = 6 units

Therefore,

Perimeter = 2(3+6) = 2(9) = 18

Thus perimeter of rectangle is 18 units