Question

I have a stream with three components, A, B, and C, coming from another process. The stream is 50 % A, and the balance is equal parts B & C, on a molar basis. These three components will undergo a reaction when fed into a reactor. The reaction is A+2B 4C-> 2x + 3Y The product Y is an important product, and so we want to maximize (to the extent possible) the conversion to Y. What must the conversion of the limiting reagent be in order to have the molar fraction of Y in the outlet stream from the reactor be 0.10?

Answer 1

`X_(A) = (N_(Ao)-N_(A))/(N_(Ao))`

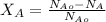
Nₐ₀-Nₐ = 1.33

Nₐ₀ = 2.5

Conversion X = 1.33/2.5 = 0.533

Step-by-step explanation:

A + 2B + 4C ⇒ 2X + 3Y

Given a stream containing 50% A, 25% B and 25% C, to get the limiting reactant, lets take a simple basis

Say stream is 10 moles, this give

A = 5moles

B = 2.5mole

C = 2.5moles

from the balanced equation above,

1mole of A ⇒ 4moles of C

∴ 5moles of A ⇒ (5x4)/1 ⇒ 20moles of C

also;

2mole of B ⇒ 4moles of C

∴ 2.5moles of B ⇒ (2.5x4)/2 ⇒ 5moles of C

so clearly from above reactant C is the limiting reactant.

Note: To get conversion of a process, we must use the limiting reactant. this is because ones it is used up, the reaction comes to an end

Formula to obtain conversion is:

Conversion = (Amount of A used up)/(Amount of A fed into the system)

`X_(A) = (N_(Ao)-N_(A))/(N_(Ao))`

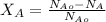
where, Nₐ₀-Nₐ = is the amount in moles of A used up

Nₐ₀ = amount in moles of A fed into the system

The next question is what mole of reactant C will give 0.1mole fraction of Y

Recall our basis = 10moles

from conservation of mass law, 10mole of product must come out which 0.1 moles fraction is Y

therefore amount Y in the product is = 0.1x10 = 1mole

if 3moles of Y ⇒ 4mole of C

∴ 1mole of Y ⇒ (1x4)/3 ⇒ 1.33moles of C

calculating the conversion of limiting reactant C that will give 0.1mole fraction of Y

Nₐ₀-Nₐ = 1.33

Nₐ₀ = 2.5

Conversion X = 1.33/2.5 = 0.533