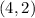Question

Solve this system of linear equations. Separate

the x. and y-values with a comma.
9x = 48 - by
5x = 8 + 6y
Enter the correct answer.

Answer 1

Answer:
`(4,2)`

Explanation:

The first equation is actually
`9x = 48 - 6y`

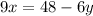
Given the following System of equations:

`\left \{ {{9x = 48 - 6y} \atop {5x = 8 + 6y}} \right.`

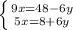
You can apply the Elimination method to solve it:

1. In this case you can start by adding both equations.

2. Then you must solve for the variable "x" in order to find its value.

You get:

`\left \{ {{9x = 48 - 6y} \atop {5x = 8 + 6y}} \right.\\...................\\14x=56\\\\x=(56)/(14)\\\\x=4`

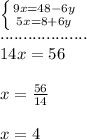
3. Now, knowing the value of the variable "x", you can substitute it into any original equation.

4. Finally, solve for "y" in order to calculate its value.

You get that this is:

`5x = 8 + 6y\\\\5(4) = 8 + 6y\\\\20=8+6y\\\\20-8=6y\\\\12=6y\\\\(12)/(6)=y\\\\y=2`

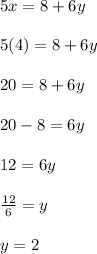
Then the solution in the form
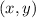`(x,y)`, is:

`(4,2)`