A. The angle formed by the base of the ladder and level ground is 56.442°.
B. The angle formed between the top of the ladder and the window is 33.588°.
C. The distance between the base of the ladder and the house is 13.266 feet.
Explanation:
Step 1; We can form a right-triangle from the given data. The opposite side has a length of 20 feet, the hypotenuse of the triangle measures 24 feet. We can determine the angle of the triangle using the given lengths. Assume the angle between the base of the ladder and the ground is x. To calculate the sine of angle x we divide the opposite side by the hypotenuse side.
sin x =
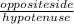 =
=
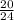 = 0.8333.
= 0.8333.
x =
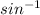 (0.8333), x = 56.442°.
(0.8333), x = 56.442°.
Step 2; Assume the angle made by the top of the ladder and the second story window is y. All triangles have a total angle of 180°. So we have one angle as 56.442° and as it is a right-triangle, another angle is 90°. So
y° + 56.442° + 90° = 180°, y = 180° - ( 90° + 56.442°) = 180° - 146.442° = 33.588°.
So y = 33.588°.
Step 3; According to Pythagoras' theorem;
the hypotenuse' length² = the opposite side's length² + the adjacent side's length².
The hypotenuse' length is given as 24 feet and the opposite side's length is given as 20 feet. Assume the adjacent side's length to be A.
24² = 20² + A², A² = 24² - 20² = 576 - 400 = 176.
A² = 176, A = 13.266 feet.