Question

You are testing a new amusement park roller coaster with an empty car with a mass of 108kg. One part of the track is a vertical loop with a radius of 12.0m. At the bottom of the loop (pointA) the car has a speed of 25.0m/sand at the top of the loop (pointB) it has speed of 8.00m/s.

As the car rolls from point A to point B, how much work is done by friction?

Answer 1

The work done is - 4892 J. And the work is negative because it is done against the motion of the car.

Step-by-step explanation:

The mechanical energy of the car at point A is

`E_(A) = (1)/(2) mv_(A)^2 + mgh_(A)`

where

m = 108 kg is the mass of the car

`v_(A)` = 25 m/s is the speed at point A

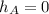`h_(A) = 0` is the height of the car at point A (zero because it is at the bottom of the loop)

Substituting into the equation, we find

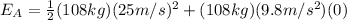`E_(A) = (1)/(2) (108 kg) (25 m/s)^2 + (108 kg) (9.8 m/s^2)(0)` = 33750 J.

The mechanical energy of the car at point B is

`E_(B) = (1)/(2) mv_(B) ^2 + mgh_(B)`

where

m = 108 kg is the mass of the car

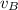`v_(B)` = 8.0 m/s is the speed at point B

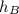`h_(B)` = 24.0 m (twice the radius) is the height of the car at point B, at the top of the loop.

Substituting into the equation, we find

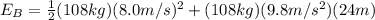`E_(B) = (1)/(2) (108 kg)(8.0 m/s)^2 + (108 kg)(9.8 m/s^2)(24 m)` = 28858 J.

So, the work done by friction is

`W = E_(B) - E_(A)` = 28858 J - 33750 J = - 4892 J.

And the work is negative because it is done against the motion of the car.