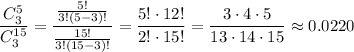Question

The 2003 Zagat Restaurant Survey provides food, decor, and service ratings for some of the top restaurants across the United States. For 15 top-ranking restaurants located in Boston, the average price of a dinner, including one drink and tip, was $48.60. You are leaving on a business trip to Boston and will eat dinner at three of these restaurants. Your company will reimburse you for a maximum of $50 per dinner. Business associates familiar with the restaurants have told you that the meal cost at 5 of the restaurants will exceed $50. Suppose that you randomly select three of these restaurants for dinner.

a. What is the probability that none of the meals will exceed the cost covered by your company (to 4 decimals)?
b. What is the probability that one of the meals will exceed the cost covered by your company (to 4 decimals)?
c. What is the probability that two of the meals will exceed the cost covered by your company (to 4 decimals)?
d. What is the probability that all three of the meals will exceed the cost covered by your company (to 4 decimals)?

Answer 1

See explanation

Explanation:

5 of 15 top-ranking restaurants offer dinner for more than $50 and 10 offer dinner for less than $50.

You will eat dinner at three of these restaurants.

a) The probability that none of the meals will exceed the cost covered by your company is

`(C^(10)_3)/(C^(15)_3)=((10!)/(3!(10-3)!))/((15!)/(3!(15-3)!))=(10!\cdot 12!)/(7!\cdot 15!)=(8\cdot 9\cdot 10)/(13\cdot 14\cdot 15)\approx 0.2637`

b) The probability that one of the meals will exceed the cost covered by your company is

`(C^(10)_2\cdot C^5_1)/(C^(15)_3)=((10!)/(2!(10-2)!)\cdot (5!)/(1!(5-1)!))/((15!)/(3!(15-3)!))=(10!\cdot 5!\cdot 3!\cdot 12!)/(2!\cdot 8!\cdot 4!\cdot 15!)=( 9\cdot 10\cdot 5\cdot 3)/(\cdot 13\cdot 14\cdot 15)\approx 0.4945`

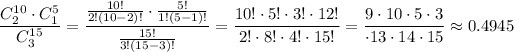
c) The probability that two of the meals will exceed the cost covered by your company is

`(C^(10)_1\cdot C^5_2)/(C^(15)_3)=((10!)/(1!(10-1)!)\cdot (5!)/(2!(5-2)!))/((15!)/(3!(15-3)!))=(10!\cdot 5!\cdot 3!\cdot 12!)/(9!\cdot 2!\cdot 3!\cdot 15!)=(10\cdot 3\cdot 4\cdot 5)/(13\cdot 14\cdot 15)\approx 0.2198`

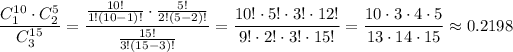
d) The probability that all three of the meals will exceed the cost covered by your company is

`(C^(5)_3)/(C^(15)_3)=((5!)/(3!(5-3)!))/((15!)/(3!(15-3)!))=(5!\cdot 12!)/(2!\cdot 15!)=(3\cdot 4\cdot 5)/(13\cdot 14\cdot 15)\approx 0.0220`