Answer:
The new fundamental frequency will be 598.7Hz.
Step-by-step explanation:
The fundamental wavelength of the sound waves in the soda bottle is given by the equation
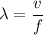
where
 is the speed of sound, and
is the speed of sound, and
 is the frequency. Since
is the frequency. Since
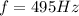 and
and
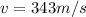 , we have
, we have

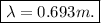
Because it is a fundamental wavelength, the length
 of the soda can must be
of the soda can must be

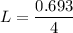
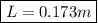
The length of the soda bottle is 0.173 meters.
Now, if we pour 0.030 m of water, the new length of the air cavity becomes
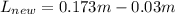
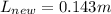
Therefore, the new fundamental wavelength will be

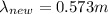 ,
,
which is a frequency of
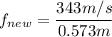

Thus, the new fundamental frequency is 598.7Hz.