Question

Particles of m1 and m2 (m2>m1) are connected by a line in extensible string passing over a smooth fixed pulley. Initially, both masses hang vertically with mass m2 at a height x above the floor. If the system is released from rest, with what speed will mass m2 hit the floor and the mass will rise a further distance (m2-m1) x) /m1+m2 after this occurs ​

​

Answer 1

The velocity with which the mass will hit the floor is
`v_f = \sqrt{2((m_2-m_1)/(m_2+m_1)) x.}`

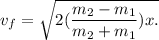
Step-by-step explanation:

If the tension in the string is
`T`, for
`m_1` we have

`T- m_1g =m_1a`,

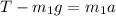and for the mass
`m_2`

`T -m_2g = -m_2a`

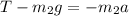
From these equations we solve for
`a` and get:

`a =((m_2-m_1)/(m_2+m_1)) g.`

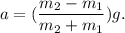
The kinematic equation

`v_f^2 = v_0^2+2ax`

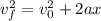
gives the final velocity
`v_f` of a particle, when its initial velocity was
`v_0`, and has traveled a distance
`x` while undergoing acceleration
`a`.

In our case

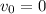`v_0 = 0` (the initial velocity of the particles is zero)

`a =((m_2-m_1)/(m_2+m_1)) g.`

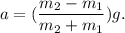
which gives us

`v_f^2 = 2ax`

`v_f^2 =2((m_2-m_1)/(m_2+m_1)) g`

`\boxed{v_f = \sqrt{2((m_2-m_1)/(m_2+m_1)) x.} }`

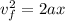
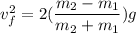
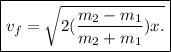
which is the velocity with which the mass
`m_2` will hit the floor.