Answer:
- (b) E(p) = 17,600 – 2400p
- (c) R(p) = –1,200p² + 7,800p
- (d) See the graph attached:
- The price that yields the maximum revenue is $3.25
- The revenue at that price is $12,675
- The prices at the breakeven points are $2.41 and $6.09
Step-by-step explanation:
1. Data:
- i) Unit variable cost: $2.00/u
- iii) Demand function: q = –1,200p + 7,800 (p is the price, q is the quantity demanded)
2. Solution
a. Write the expense equation in terms of the demand q.
- Total cost = fixed costs + variable cost
- Variable costs = quanity × unit variable cost
- Total cost = $2,000 + q × $2/u
- Expense equation: E(q) = 2,000 + 2q ← answer
b. Express the expense equation from part a in terms of the price p
This is a composition of functions.
- Expense equation, E(p) = E[q(p)]
- E[q(p)] = 2,000 + 2(–1,200p + 7,800)
- E[q(p)] = 2,000 – 2400p + 15,600 = 17,600 – 2400p
- E[q(p)] = 17,600 – 2400p = E(p)
c. Write the revenue function in terms of the price.
Revenue is the product of the quantity demanded and the price
- R(p) = p × q = p × [ –1,200p + 7,800]
d. Graph the functions in an appropriate viewing window.
To draw the revenue function take into account:
- It is a parabola
- It opens downward
- The y-intercept is (0,0) [you caluate it when p = 0]
- The xintercpets are (0,0) and (0,6.5)
- The vertex is at p equal to the midpoint between the two x-intercepts:
p = (0 + 6.5)/2 = 3.25
- What price yields the maximum revenue?
p = 3.25
- What is the revenue at that price?
R(3.25) = - 1200(3.25)² + 7800(3.25) = 12,675
To draw the expense function:
- It is a line
- the y-intercept is (0, 17600) [make p = 0 in the equation]
- the x-intercept is (7.33,0) [make E(p) = 0 in the equation)
- Identify the price at the breakeven points. and Round answers to the nearest cent.
The breakeven points are when the two functions intersect. They corresponding p values are.
Thus they are the solutions to the equation:
- -1200p² + 7800p = 17600 - 2400p
- 1200p² -10200p + 17600 =0
Use the quadratic equation:
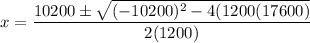
The solutions are also shown on the graph: