Question

A machine that produces ball bearings has initially been set so that the mean diameter of the bearings it produces is 0.500 inches. A bearing is acceptable if its diameter is within 0.004 inches of this target value. Suppose, however, that the setting has changed during the course of production, so that the distribution of the diameters produced is now approximately normal with mean 0.499 inch and standard deviation 0.002 inch. What percentage of the bearings produced will not be acceptable

Answer 1

7.3% of the bearings produced will not be acceptable.

Explanation:

We are given the following information in the question:

Mean, μ = 0.499 inch

Standard Deviation, σ = 0.002 inch

We are given that the distribution of the diameters is a bell shaped distribution that is a normal distribution.

Formula:

`z_(score) = \displaystyle(x-\mu)/(\sigma)`

A bearing is acceptable if its diameter is within 0.004 inches that is the range is from 0.496 inch to 0.504 inches.

P(diameter between 0.496 inch and 0.504 inch)

`P(0.496 \leq x \leq 0.504) = P(\displaystyle(0.496 - 0.499)/(0.002) \leq z \leq \displaystyle(0.504-0.499)/(0.002)) = P(-1.5 \leq z \leq 2.5)\\\\= P(z \leq 2.5) - P(z < -1.5)\\= 0.994 - 0.067 = 0.927= 92.7\%`

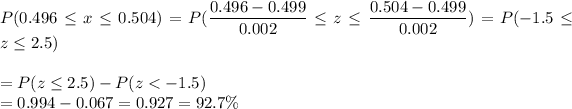
Percentage of the bearings produced will not be acceptable =

`100-92.7\\=7.3\%`

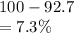
Thus, 7.3% of the bearings produced will not be acceptable.