Question

The solar wind is a thin, hot gas given off by the sun. Charged particles in this gas enter the magnetic field of the earth and can experience a magnetic force. Suppose a charged particle traveling with a speed of 7.25 x 106 m/s encounters the earth's magnetic field at an altitude where the field has a magnitude of 1.37 x 10-7 T. Assuming that the particle's velocity is perpendicular to the magnetic field, find the radius of the circular path on which the particle would move if it were (a) an electron and (b) a proton.

Answer 1

Step-by-step explanation:

speed of the charged particle, v = 7.25 x 10^6 m/s

magnetic field of earth, B = 1.37 x 10^-7 T

mass of electron, me = 9.1 x 10^-31 kg

mass of proton, mp = 1.67 x 10^-27 kg

charge on electron or proton, q = 1.6 x 10^-19 C

The magnetic force is balanced by the centripetal force.

`qvB = (mv^(2))/(r)`

`r=(mv)/(Bq)`

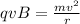
where, r is the radius of the circular path

(a)

For the electron

`r=(9.1*10^(-31)* 7.25* 10^(6))/(1.37* 10^(-7)* 1.6*10^(-19))`

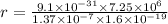
r = 30.1 m

(b)

for proton

`r=(1.67*10^(-27)* 7.25* 10^(6))/(1.37* 10^(-7)* 1.6*10^(-19))`

r = 5.52 x 10^5 m

Answer 2

Step-by-step explanation:

Charge on the particle = 1.6 x 10⁻¹⁹ C

mass of electron = 9.1 x 10⁻³¹ kg

mass of proton = 1.67 x 10⁻²⁷ kg

A charged particle moves in a magnetic field on circular path so that magnetic force = mv² /r

B q v = mv² /r , B is magnetic field

r = mv / qB

For proton

r = (1.67 x 10⁻²⁷ x 7.25 x 10⁶) / (1.6 x 10⁻¹⁹ x 1.37 x 10⁻⁷)

= 5.5 x 10⁵ m

For electron

r = (9.1 x 10⁻³¹ x 7.25 x 10⁶) / (1.6 x 10⁻¹⁹ x 1.37 x 10⁻⁷)

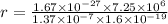
= 30.1 x 10

= 301 m