Given Information:
Area of rectangle = 16 square feet
Required Information:
Least amount of material = ?
Answer:
x = 4 ft and y = 4 ft
Explanation:
We know that a rectangle has area = xy and perimeter = 2x + 2y
We want to use least amount of material to design the sandbox which means we want to minimize the perimeter which can be done by taking the derivative of perimeter and then setting it equal to 0.
So we have
xy = 16
y = 16/x
p = 2x + 2y
put the value of y into the equation of perimeter
p = 2x + 2(16/x)
p = 2x + 32/x
Take derivative with respect to x
d/dt (2x + 32/x)
2 - 32/x²
set the derivative equal to zero to minimize the perimeter
2 - 32/x² = 0
32/x² = 2
x² = 32/2
x² = 16
x =
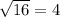 ft
ft
put the value of x into equation xy = 16
(4)y = 16
y = 16/4
y = 4 ft
So the dimensions are x = 4 ft and y = 4 ft in order to use least amount of material.
Verification:
xy = 16
4*4 = 16
16 = 16 (satisfied)