Question

If it requires 8.0 J of work to stretch a particular spring by 2.0 cm from its equilibrium length, how much more work will be required to stretch it an additional 4.0 cm? Express your answer to two significant figures and include the appropriate units.

Answer 1

The amount of work done required to stretch spring by additional 4 cm is 64 J.

Step-by-step explanation:

The energy used for stretching spring is given by the relation :

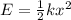`E = (1)/(2)kx^(2)` .......(1)

Here k is spring constant and x is the displacement of spring from its equilibrium position.

For stretch spring by 2.0 cm or 0.02 m, we need 8.0 J of energy. Hence, substitute the suitable values in equation (1).

`8 = (1)/(2)*k* k *(0.02)^(2)`

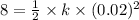
k = 4 x 10⁴ N/m

Energy needed to stretch a spring by 6.0 cm can be determine by the equation (1).

Substitute 0.06 m for x and 4 x 10⁴ N/m for k in equation (1).

`E = (1)/(2)*4*10^(4)* (0.06)^(2)`

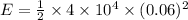
E = 72 J

But we already have 8.0 J. So, the extra energy needed to stretch spring by additional 4 cm is :

E = ( 72 - 8 ) J = 64 J