The slope of the line joining the points (-1,5) and (6,-2) is -1
x + y = 4 is the equation of line
x intercept is (-4, 0)
y intercept is (0, 4)
Solution:
Given that,
Points are (-1,5) and (6,-2)
The slope of line is given as:
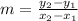
From given,
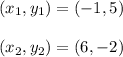
Substituting the values we get,
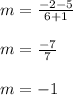
Thus slope of line is -1
The equation of line in slope intercept form is given as:
y = mx + c -------- eqn 1
Where,
m is the slope
c is the y intercept
Substitute m = -1 and (x, y) = (-1, 5) in eqn 1
5 = -1(-1) + c
5 = 1 + c
c = 4
Substitute m = -1 and c = 4 in eqn 1
y = -x + 4
In standard form,
x + y = 4 is the equation of line
Find x intercept:
Substitute y = 0
x + 0 = 4
x = -4
Thus x intercept is (-4, 0)
Find y intercept:
Substitute x = 0
0 + y = 4
y = 4
Thus y intercept is (0, 4)