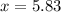The x - coordinate of the solution is
Step-by-step explanation:
The two equations are
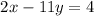 and
and
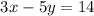
The image attached below shows the solution of the two equations.
The x - coordinate of the solution can be determined using substitution method.
Let us substitute
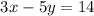 ⇒
⇒
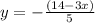 in the equation
in the equation
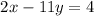
Thus, we have,

Simplifying, we get,
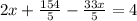
Adding the like terms, we have,
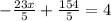
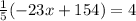
Multiplying both sides by 5, we have,
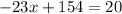
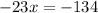
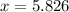
Rounding off to the nearest hundredth, we get,
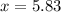
Hence, the x - coordinate of the solution is