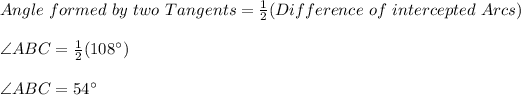Answer: SECOND OPTION.
Explanation:
By definition, the Angle Formed the by the intersection of two Tangents outside of a circle can be calculated with the following formula:
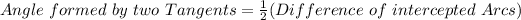
In this case, based on the information you provided in the exercise, we know that:

Knowing those values, you can substitute them into the formula, you get: