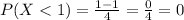Question

Consider a uniform distribution that is defined for 1 ≤ X ≤ 5 . a. Sketch the distribution. b. What is the probability that X falls below 1.5? c. What is the probability that X lies above 2.5? d. What

Answer 1

a)
`X \sim Unif(a= 1, b=5)`

The density function for this case is given by:

`f(X) = (1)/(b-a)= (1)/(5-1)= (1)/(4) , 1\leq X \leq 5`

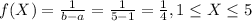
And the distribution is on the figure attached

b)
`P(X <1.5)`

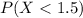
And for this case we can use the cumulative distribution function given by:

`F(x) = (x-a)/(b-a)= (x-1)/(5-1)= (x-1)/(4), 1\leq X \leq 5`

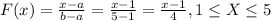
And if we use this formula we got:

`P(X<1.5) = (1.5-1)/(4)= (0.5)/(4)= (1)/(8)=0.125`

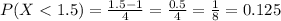
c)
`P(X >2.5)`

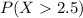
And we can use the complement rule and the cimulative distribution function and we can rewrite the expression like this:

`P(X >2.5) = 1-P(X<2.5) = 1-F(2.5) = 1-(2.5-1)/(5-1)= 1-(1.5)/(4)= 1-(3)/(8)= (5)/(8)=0.625`

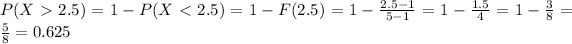
d)
`P(X<1) = (1-1)/(4)= (0)/(4)= 0`

Explanation:

Part a

For this case we define the random variable X and the distribution for X is given by:

`X \sim Unif(a= 1, b=5)`

The density function for this case is given by:

`f(X) = (1)/(b-a)= (1)/(5-1)= (1)/(4) , 1\leq X \leq 5`

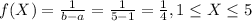
And the distribution is on the figure attached

Part b

For this case we want this probability:

`P(X <1.5)`

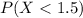
And for this case we can use the cumulative distribution function given by:

`F(x) = (x-a)/(b-a)= (x-1)/(5-1)= (x-1)/(4), 1\leq X \leq 5`

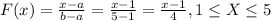
And if we use this formula we got:

`P(X<1.5) = (1.5-1)/(4)= (0.5)/(4)= (1)/(8)=0.125`

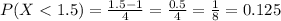
Part c

For this case we want this probability:

`P(X >2.5)`

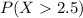
And we can use the complement rule and the cimulative distribution function and we can rewrite the expression like this:

`P(X >2.5) = 1-P(X<2.5) = 1-F(2.5) = 1-(2.5-1)/(5-1)= 1-(1.5)/(4)= 1-(3)/(8)= (5)/(8)=0.625`

Part d" What is the probability that X lies below 1?

`P(X <1)`

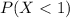
And for this case we can use the cumulative distribution function given by:

`F(x) = (x-a)/(b-a)= (x-1)/(5-1)= (x-1)/(4), 1\leq X \leq 5`

And if we use this formula we got:

`P(X<1) = (1-1)/(4)= (0)/(4)= 0`