Answer:
The third sequence.
Explanation:
In an arithmetic sequence, the difference between two consecutive terms is the same.
For each option, find the difference between consecutive terms:
First option:
The differences are not the same. As a result, this option is not an arithmetic sequence.
Second option:
The differences are not the same. As a result, this option is not an arithmetic sequence, either.
Third option:
The differences are all
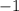 . As a result, this option is indeed an arithmetic sequence. Its common difference is
. As a result, this option is indeed an arithmetic sequence. Its common difference is
 .
.
Fourth option:
The differences are varying between
 and
and
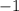 . As a result, this option is not an arithmetic sequence.
. As a result, this option is not an arithmetic sequence.