Question

A basketball player shoots a basketball with an initial velocity of 15 ft/sec. The ball is released from an initial height of 6.5 feet. PLEASE HELP

Answer 1

A basketball player shoots a basketball with an initial velocity of 15 ft/sec. The ball is released from an initial height of 6.5 feet.

The function
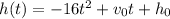`h(t) =-16t^2+v_0t+h_0` models the height, in feet, of an object after t seconds.
`v_0` is the initial velocity of the object, and
`h_0` is the initial height of the object.

Part 1: Write a function that models the height of the basketball. Use your function to answer Parts 2-4.

Part 2: How long does it take for the basketball to hit the ground? Round your answer to the nearest hundredth. Show all of your work. You're welcome to use this quadratic formula calculator, but please explain your answer. (Links to an external site.)

Part 3: When does the basketball reach its maximum height? Round your answer to the nearest hundredth. Show all of your swork and explain your answer.

Part 4: What is the maximum height of the basketball? Round your answer to the nearest hundredth. Show all of your work and explain your answer.

The answers to the question is

Part 1

`h(t) =-16t^2+15t+6.5`

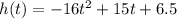
Part 2

It takes 6.5 s for the basketball to hit the ground

Part 3

The basketball reaches its maximum height at 0.47 s from the start

Part 4

The maximum height reached by the basketball is 9.41 ft

Explanation:

Part 1

The function that models the height of the ball in the question is

`h(t) =-16t^2+15t+6.5`

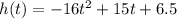
Part 2

At ground level h(t) = 0 therefore
`0 =-16t^2+15t+6.5`

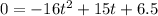
Factorizing gives -(t - 6.5) = 0 or t = 6.5 s

Part 3

The maximum height is reached at the tip of the parabola where t = -b/(2a)

where a = -16 and b = 15 therefore t = 15/32 s = 0.46875 s or 0.47 s to the nearest hundreth

Part 4

The maximum height becomes -16×(15/32)² + 15×15/32+ 6.5 = 9.413 ft