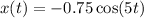Answer:
(a) 0.126 s
(b) Maximum speed = 0.15 m/s
Maximum acceleration = 0.75 m/s2
(c) Position:
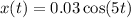
Velocity:

Acceleration:
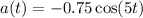
Step-by-step explanation:
(a) The motion is a simple harmonic motion. For a loaded spring, it's period, T, is given by
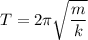
m and k are, respectively, the mass of the load and the force constant of the spring.
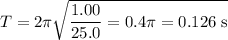
(b) The maximum speed is given by
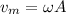 and maximum acceleration by
and maximum acceleration by
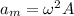
where
 is the angular velocity and A is the amplitude or maximum displacement from the equilibrium or central point.
is the angular velocity and A is the amplitude or maximum displacement from the equilibrium or central point.
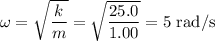
A = 3 cm = 0.03 m
Hence,
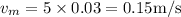
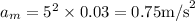
(c) The general equation of SHM is
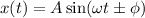
x(t) is the position at time, t
 is the angular velocity
is the angular velocity
T is the time
 is the phase difference which determines at what point the oscillation began. If it begins at the middle (which is almost practically impossible), it's value is 0. If it begins at any endpoint (which is most practical), its value is
is the phase difference which determines at what point the oscillation began. If it begins at the middle (which is almost practically impossible), it's value is 0. If it begins at any endpoint (which is most practical), its value is
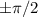 , the sign depending on which side of the equilibrium point it begins from.
, the sign depending on which side of the equilibrium point it begins from.
By trigonometry,
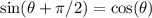 .
.
Putting all values in x(t),
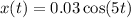
Velocity is the time-derivative of position. Hence,

Acceleration is the time-derivative of velocity. Hence,