Answer:
v = 21.127 m/s
Step-by-step explanation:
Let's start off with the equation for centrifugal force:
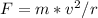
This force has to be equal to the force of friction which is:
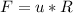 (where u = coefficient of friction and R = mass * gravity )
(where u = coefficient of friction and R = mass * gravity )
Assumption: The car is travelling on horizontal ground
We can set the above equations equal to one another to get:
(m*v^2)/r = u * (m * 9.81)
here u = 0.7
r = 65
and mass cancels out on each side
Solving for v, we get:
v = 21.127 m/s