Question

A battery with an internal resistance ofrand an emf of 10.00 V is connected to a loadresistorR=r. As the battery ages, the internal resistance triples. How much is thecurrent trough the load resistor reduced? Explain.

Answer 1

The current is reduced to half of its original value.

Step-by-step explanation:

• Assuming we can apply Ohm's Law to the circuit, as the internal resistance and the load resistor are in series, we can find the current I₁ as follows:

`I_(1) = (V)/(R_(int) +r_(L) )`

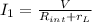
• where Rint = r and RL = r
• Replacing these values in I₁, we have:

`I_(1) = (V)/(R_(int) +r_(L) ) = (V)/(2*r) (1)`

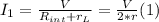
• When the battery ages, if the internal resistance triples, the new current can be found using Ohm's Law again:

`I_(2) = (V)/(R_(int) +r_(L) ) = (V)/((3*r) +r) = (V)/(4*r) (2)`

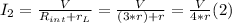
• We can find the relationship between I₂, and I₁, dividing both sides, as follows:

`(I_(2) )/(I_(1) ) = (V)/(4*r) *(2*r)/(V) = (1)/(2)`

• The current when the internal resistance triples, is half of the original value, when the internal resistance was r, equal to the resistance of the load.