Question

A plane flying over the ocean is on course to land on an aircraft carrier. The diagonal distance between the plane and the aircraft carrier is 10 miles. If the plane needs to maintain a constant descent angle of 20° with the horizontal to land on the aircraft carrier, then what is the plane's current height above the ocean in miles?

Answer 1

the plane's current height above the ocean is 3.42 miles

Explanation:

Given that the diagonal distance between the plane and the aircraft carrier is 10 miles.

What we need to find is the vertical distance between the plane and the aircraft carrier which is the plane's current height above the ocean. This can be gotten using sine rule.

For sine rule, you need a side and its opposite angle. For this question the triangle formed is a right angle triangle with diagonal distance, vertical distance and horizontal distance.

let a = diagonal distance = 10 miles

let the opposite angle to the diagonal distance be A = 90° (right angle)

let the vertical distance = b

let the opposite angle to the vertical distance be B = 20°

Sine rule states that
`(a)/(sin(A)) = (b)/(sin(B))`

∴
`(10)/(sin(90)) = (b)/(sin(20))`

`b = sin(20)(10)/(sin(90))`

`b = 0.342*(10)/(1)`

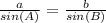
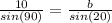
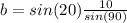
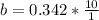
⇒ b = 3.42 miles

Therefore the plane's current height above the ocean is 3.42 miles