Question

A water-skier is moving at a speed of 14.3 m/s. When she skis in the same direction as a traveling wave, she springs upward every 0.450 s because of the wave crests. When she skis in the direction opposite to that in which the wave moves, she springs upward every 0.342 s in response to the crests. The speed of the skier is greater than the speed of the wave. Determine (a) the speed and (b) the wavelength of the wave.

Answer 1

When the skier skis in the same direction as the wave, the wavelength of the wave is 6.435 m. When the skier skis in the opposite direction, the wavelength of the wave is 4.897 m.

Step-by-step explanation:

To determine the speed and wavelength of the wave, we can use the equation v = λ/T, where v is the speed, λ is the wavelength, and T is the period. Let's consider when the water-skier is skiing in the same direction as the wave first.

Given that the skier springs upward every 0.450 s and the speed of the skier is 14.3 m/s, we can substitute these values into the equation. Solving for λ, we get:

λ = v * T

λ = (14.3 m/s)*(0.450 s)

λ = 6.435 m

So, the wavelength of the wave when the skier skis in the same direction is 6.435 m.

We can repeat the same process when the skier skis in the opposite direction. Given that the skier springs upward every 0.342 s and the speed of the skier is 14.3 m/s, we can substitute these values into the equation. Solving for λ, we get:

λ = v * T

λ = (14.3 m/s)*(0.342 s)

λ = 4.897 m

So, the wavelength of the wave when the skier skis in the opposite direction is 4.897 m.

Answer 2

a) 1.95 m/s

b) 5.56 m

Step-by-step explanation:

Given that:

Velocity of the skier
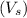`(V_s)` = 14.3 m/s

For the skier moving in the direction of the wave, we have:

Period (T) = 0.450 s

Relative velocity (V) of the skier in regard with the wave =
`(V_s - V_w)`

where:

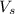`V_s` = velocity of the skier

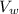`V_w` = velocity of the wave

The wavelength
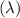`(\lambda)` can be written as:

`\lambda = (V_s-V_w)T`

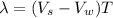
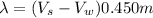`\lambda = (V_s-V_w) 0.450m` ---------------> Equation (1)

For the skier moving opposite in the direction of the wave, we have:

Period (T) = 0.342 s

Relative velocity (V) of the skier in regard with the wave =
`(V_s + V_w)`

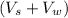
The wavelength
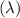`(\lambda)` can be written as:

`\lambda = (V_s+V_w)T`

`\lambda = (V_s+V_w) 0.342m` ------------------> Equation 2

Equating equation (1) and equation (2) and substituting
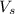`V_s` = 14.3 m/s ; we have:

`(V_s-V_w) 0.450m = (V_s-V_w) 0.342m`

`0.450m(V_s)-0.450m(V_w) = 0.342m(V_s)+0.342m(V_w)`

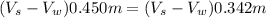
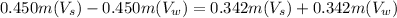
Collecting the like terms; we have:

`0.450m(V_s) - 0.342m(V_s) = 0.342m(V_w)+0.450m(V_w)`

`(V_s)(0.450m - 0.342m) = (V_w)0.342m+0.450m`

`14.3m/s(0.450m - 0.342m) = (V_w)0.342m+0.450m`

`14.3m/s(0.108m = (V_w)0.792m`

`1.5444m^2/s = (V_w)0.792m`

`(V_w) = (1.5444m^2/s)/( 0.792m)`

`(V_w) = 1.95 m/s`

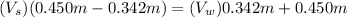
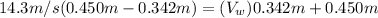
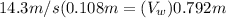
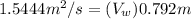
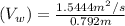
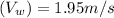
b)

The Wavelength of the wave can be calculated using :
`( \lambda }) = (V_s-V_w) 0.450m`

`({\lambda}) = (14.3 m/s -1.95 m/s)(0.450)`

`(\lambda) = (12.35)0.450m`

`(\lambda)= 5.5575 m`

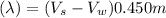
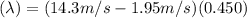
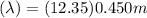
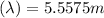
λ ≅ 5.56 m