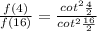Question

A beam of 3 MeV α particles scatters from a thin gold foil. What is the ratio of the number of α particles scattered to angles greater than 4° to the number scattered to angles greater than 16°?

Answer 1

Ratio of number of alpha particles is 16.20

Step-by-step explanation:

In Rutherford Scattering, the fraction of incident beam particles scattered with angle θ and grater than θ is given by the relation :

`f(\theta)=\pi nt((Z_(1)Z_(2)e^(2) )/(8\pi\epsilon_(0)K ) )^(2) \cot^(2)(\theta)/(2)`

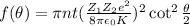
Here Z₁ is the atomic number of target, Z₂ is atomic number of incident particles, e is electronic charge, K is kinetic energy of incident particles, n is target particle density and t is thickness of the target foil.

According to the problem, number of alpha scattered to angles greater than 4° is given by the relation :

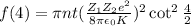`f(4)=\pi nt((Z_(1)Z_(2)e^(2) )/(8\pi\epsilon_(0)K ) )^(2) \cot^(2)(4)/(2)` ....(1)

Number of alpha scattered to angles greater than 16° is given by the relation :

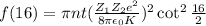`f(16)=\pi nt((Z_(1)Z_(2)e^(2) )/(8\pi\epsilon_(0)K ) )^(2) \cot^(2)(16)/(2)` .....(2)

Ratio of equation (1) and (2) gives :

`(f(4))/(f(16)) =(cot^(2)(4)/(2))/(cot^(2)(16)/(2))`

`(f(4))/(f(16)) =16.20`