Answer:
Question 1.
- a)
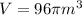
- b)
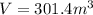
Question 2:
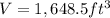
Question 3:

Step-by-step explanation:
Question 1. In the cone below, the radius is 6 meters and the height is 8 meters.
A) Find the exact value of the volume of the cone.
Formula:

Plug in r = 6m, and h = 8m
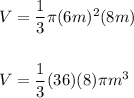
Solution:
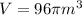
B) Find the approximate value of the volume of the cone rounded to the nearest tenth.
Substitute π with its approximate value 3.14

Question 2. Find the volume of the cylinder pictured below. Use 3.14 for pi. Give your answer rounded to the nearest tenth.
Formula

Plug in diameter = 10 ft, height = 21, and π = 3.14

Solution:
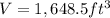
Question 3. Find the volume of the sphere pictured below. The sphere has a radius of 20 cm. Use 3.14 for pi. Give your answer rounded to the nearest tenth.
Formula

Plug in r = 20cm, and π = 3.14
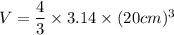
Solution:
