Question

A toy manufacturer interviews eight people for four openings in the research and development department of the company. Three of the eight people are women. If all eight are qualified, in how many ways can the employer fill the four positions if (a) the selection is random and (b) exactly two selections are women?

Answer 1

This can be solved using Combination.

Explanation:

Using combination principle ⁿCₐ =
`(n!)/((n-a)!a!)`

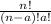
Given that;

n = total number of items available

a = number of items being chosen

The total number of candidates = 8

Women candidates = 3

Men candidates = 5

Job openings = 4

(a.) For a random selection,

n = total number of candidates = 8

a = job openings available = 4

Possible combinations is given by

⁸C₄ =
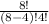`(8!)/((8-4)!4!)` = 70 ways

Hence, the employer can fill the four positions randomly in 70 possible ways.

(b.) With exactly 2 selections as women.

Then we solve the combination separately.

For women, exactly 2 is selected of 3;

³C₂ =
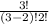`(3!)/((3-2)!2!)` = 3 ways

For men, we are left with 2 selections from 5

⁵C₂ =
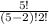`(5!)/((5-2)!2!)` = 10 ways

Hence, the possible combination is 3 x 10 = 30 ways

Hence, the employer can make exactly 2 women selections in 30 possible ways.