Answer:
A 160-V battery is connected across two parallel metal plates of area 28.5cm^2 and separation 8.20mm. A beam of alpha particles (charge +2e, mass 6.64*10^-27) is accelerated from rest through a potential difference of 1.60 kV and enters the region between the plates perpendicular to the electric field.
What magnitude of magnetic field is needed so that the alpha particles emerge undeflected from between the plates?
What direction of magnetic field is needed so that the alpha particles emerge undeflected from between the plates if the charges are moving to the right and the electric field points upward?
The answers to the question are
(a) 4.97 × 10⁻² T
(b) Perpendicularly coming out from the computer screen
Step-by-step explanation:
d = 8.20mm = 8.2×10⁻³ m
Where V₀ = Battery voltage = 160-V
The voltage of acceleration V = 1600 V
Alpha particle charge, q = 3.2×10⁻¹⁹ C +2e
Mass = 6.64×10⁻²⁷
From energy balance we have
Electric Potential Energy = Kinetic energy
That is
q·V =
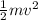which gives
v =
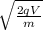
For the the case of no deflection we have
Electric force = Magnetic force
Where magnetizing force is given as q×v×B and electric force = q×E
Therefore for no deflection
q×E = q×v×B
Therefore B = E/v
and E = V₀/d
Which gives
B = V₀/d÷
=
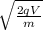
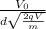
Plugging in the values, we have
B = 4.96867×10⁻² T
(B) If the charges are moving to the right and the electric field points upwards then by Flemings left hand rule the magnetic field should be perpendicular to or out from the computer monitor