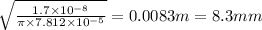Answer:
The radius of the cable is 0.0083 m or 8.3 mm.
Step-by-step explanation:
The resistance of copper cable of 1 meter length will be given by
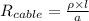 .... (i)
.... (i)
where the resistivity of copper is
 , and l is the length of the wire which is considered to be 1m, and a is the cross sectional area of the wire in
, and l is the length of the wire which is considered to be 1m, and a is the cross sectional area of the wire in
 .
.
From the formula of power we know that,
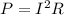 .... (ii)
.... (ii)
Therefore 2 W/m =
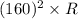 .... (iii)
.... (iii)
where the resistance,R, actually means the resistance of the cable per meter.
Therefore R ( resistance of cable per meter)
=
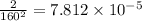 ohms / meter. .... (iv)
ohms / meter. .... (iv)
Therefore from (i)
 =
=
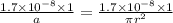 ..... (v)
..... (v)
where cross sectional area of the cable, a =
 ,
,
where r is the radius of the cable, and length of cable,l = 1m.
Therefore r =