Question

A 3.78 g bullet moving at 311 m/s penetrates a tree to a depth of 4.08 cm. Use energy considerations to find the average frictional force that stops the bullet. Answer in units of N.

Answer 1

To solve this problem we will apply the concepts related to energy conservation. In this particular case the conservation of energy is given by the conservation of the work done by the bullet and the change of the kinetic energy from the initial state (the given speed) and the final state. This way we will have to,

`W = \Delta KE`

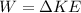
By definition work is the product between the force applied and the distance traveled, while the kinetic energy is defined as half of the product between mass and squared speed, we will have,

`Fx = (1)/(2) m\Delta v^2`

`Fx = (1)/(2) m (v_f^2-v_i^2)`

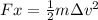
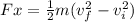
Here,

F = Force

x = Displacement

m = Mass

`v_f` = Final velocity (0m/s because there is calculated to stop it)

`v_i` = Initial Velocity

Rearranging to find the force we have that

`F = (1)/(2) (m (v_f^2-v_i^2))/(x)`

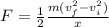
Replacing with our values

`F = (1)/(2)((3.78*10^(-3))(0^2-311^2))/(4.08*10^(-2))`

`F = -4480.45N`

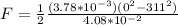
There negative sign indicates that frictional force is retar dation force.