Question

The carbon dioxide emissions of a group of nations had a mean of 8.7 and standard deviation of 2.1. a. One​ country's observation was 14.1. Find its​ z-score and interpret. b. Another​ country's observation was 2.2. Find its​ z-score and interpret. c. A third​ country's observation was 9.1. Find its​ z-score and interpret.

Answer 1

a)
`Z = 2.57`

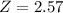
This country emmits 2.57 standard deviations above the mean of the emissions of the countries of this group of nations.

b)
`Z = -3.1`

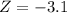
This country emmits 3.1 standard deviations below the mean of the emissions of the countries of this group of nations.

c)
`Z = 0.19`

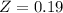
This country emmits 0.19 standard deviations above the mean of the emissions of the countries of this group of nations.

Explanation:

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

In this problem, we have that:

`\mu = 8.7, \sigma = 2.1`

a. One​ country's observation was 14.1. Find its​ z-score and interpret.

Here we have
`X = 14.1`

`Z = (X - \mu)/(\sigma)`

`Z = (14.1 - 8.7)/(2.1)`

`Z = 2.57`

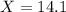
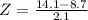
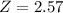
This country emmits 2.57 standard deviations above the mean of the emissions of the countries of this group of nations.

b. Another​ country's observation was 2.2. Find its​ z-score and interpret.

Here we have
`X = 2.2`

`Z = (X - \mu)/(\sigma)`

`Z = (2.2 - 8.7)/(2.1)`

`Z = -3.1`

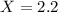
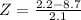
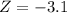
This country emmits 3.1 standard deviations below the mean of the emissions of the countries of this group of nations.

c. A third​ country's observation was 9.1. Find its​ z-score and interpret.

Here we have
`X = 9.1`

`Z = (X - \mu)/(\sigma)`

`Z = (9.1 - 8.7)/(2.1)`

`Z = 0.19`

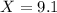
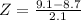
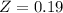
This country emmits 0.19 standard deviations above the mean of the emissions of the countries of this group of nations.