Question

g Gravel is being dumped from a conveyor belt at a rate of 40 cubic feet per minute. It forms a pile in the shape of a right circular cone whose base diameter and height are always equal. How fast is the height of the pile increasing when the pile is 25 feet high?

Answer 1

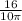`(16)/(10\pi)` feet per minute.

Step-by-step explanation:

We have been given that g Gravel is being dumped from a conveyor belt at a rate of 40 cubic feet per minute. It forms a pile in the shape of a right circular cone whose base diameter and height are always equal.

This means that 2 times radius is equal to height that is
`2r=h`.

Let us solve for radius as:

`r=(h)/(2)`

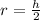
We will use cone formula to solve our given problem.

`V=(\pi r^2 h)/(3)`

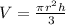
Now, we will rewrite volume function in terms of height as:

`V=(((h)/(2))^2 h\pi )/(3)`

`V=((h^2)/(4) h\pi )/(3)`

`V=(h^3\pi )/(3\cdot 4)`

`V=(\pi )/(12)\cdot h^3`

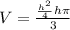
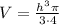
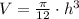
Now, we will find derivative of volume with respect to time.

`V'=(\pi )/(12)\cdot 3h^2\cdot h'`

`V'=(h^2\pi )/(4)\cdot h'`

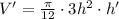
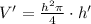
Now, we will substitute
`h=25` and
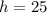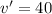`v'=40` and solve for
`h'` as:

`40=((10)^2\pi )/(4)\cdot h'`

`40=(100\pi )/(4)\cdot h'`

`40\cdot (4)/(100\pi)=(100\pi )/(4)\cdot (4)/(100\pi)\cdot h'`

`(160)/(100\pi)= h'`

`h'=(16)/(10\pi)`

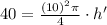
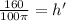
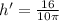
Therefore, the height of the pile is increasing at a rate of
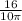`(16)/(10\pi)` feet per minute.