Question

A uniform charge density of 509 nC/m3 is distributed throughout a spherical volume of radius 6.03 cm. Consider a cubical Gaussian surface with its center at the center of the sphere. What is the electric flux through this cubical surface if its edge length is (a)4.00 cm and (b)16.8 cm?

Answer 1

Step-by-step explanation:

(a) It is known that relation between charge and volume is as follows.

`q_(enclosed) = \rho V_(cube)`

=
`(509 * 10^(-9) C/m^(3)) * (0.04 m)^(3)`

=
`509 * 10^(-9) * 6.4 * 10^(-5)`

=
`3.26 * 10^(-11) C`

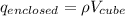
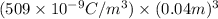
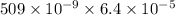
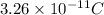
Now, according to Gauss's law

`\phi = (q_(enclosed))/(\epsilon_(o))`

=
`(3.26 * 10^(-11) C)/(8.85 * 10^(-12)C^(2)N^(-1)m^(-2))`

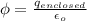
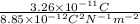
= 3.68
`N m^(2)/C`

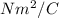
Hence, the electric flux through this cubical surface if its edge length is 4.00 cm is 3.68
`N m^(2)/C`.

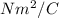(b) Similarly, we will calculate the electric flux when edge length is 16.8 cm as follows.

`q_(enclosed) = \rho V_(cube)`

=
`(509 * 10^(-9) C/m^(3)) * (0.168 m)^(3)`

=
`509 * 10^(-9) * 4.74 * 10^(-3)`

=
`2.41 * 10^(-11) C`

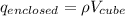
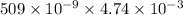
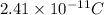
Now, according to Gauss's law

`\phi = (q_(enclosed))/(\epsilon_(o))`

=
`(2.41 * 10^(-11) C)/(8.85 * 10^(-12)C^(2)N^(-1)m^(-2))`

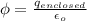
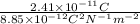
= 2.72
`N m^(2)/C`

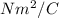
Therefore, the electric flux through this cubical surface if its edge length is 4.00 cm is 2.72
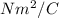`N m^(2)/C`.