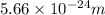Question

Calculate the wavelength of the light emitted when an electron in a one-dimensional box of length 5.4 nmnm makes a transition from the n=9n=9 state to the n=8n=8 state.

Answer 1

Answer : The wavelength of the light emitted is,
`5.66* 10^(-24)m`

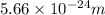
Explanation :

The energy level of quantum particle in a one-dimensional box is given as:

`E_n=(n^2h^2)/(8mL^2)`

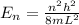
or,

`\Delta E=E_9-E_8=(n_9^2h^2)/(8mL^2)-(n_8^2h^2)/(8mL^2)`

`\Delta E=E_9-E_8=(h^2)/(8mL^2)* (n_9^2-n_8^2)`

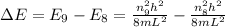
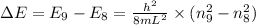
where,

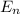`E_n` = change in energy

n = energy level

h = Planck's constant =
`6.626* 10^(-34)Js`

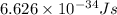
m = mass of electron =
`9.109* 10^(-31)kg`

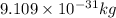
L = length of a one-dimensional box =
`5.4nm=5.4* 10^(-9)m`

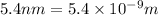
Now put all the given values in the above formula, we get:

`\Delta E=E_9-E_8=((6.626* 10^(-34)Js)^2)/(8* (9.109* 10^(-31)kg)* (5.4* 10^(-9)m)^2)* [(9)^2-(8)^2]`

`\Delta E=E_9-E_8=3.5124* 10^(-2)J`

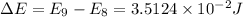
Now we have to calculate the wavelength of the light emitted.

`\Delta E=(hc)/(\lambda)`

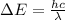
where,

h = Planck's constant =
`6.626* 10^(-34)Js`

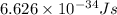
c = speed of light =
`3* 10^(8)m/s`

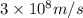
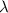`\lambda` = wavelength of the light

Now put all the given values in the above formula, we get:

`3.5124* 10^(-2)J=((6.626* 10^(-34)Js)* (3* 10^(8)m/s))/(\lambda)`

`\lambda=5.66* 10^(-24)m`

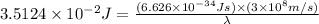
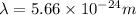
Thus, the wavelength of the light emitted is,
`5.66* 10^(-24)m`