Question

g A sample of 3 items is chosen at random from a box containing 20 items, out of which 4 are defective. Let X be the number of defective items in the sample. Find Var (X), σX, Var (20 − X) and σ20−X.

Answer 1

The variance and standard deviation of X are 0.48 and 0.693 respectively.

The variance and standard deviation of (20 - X) are 0.48 and 0.693 respectively.

Explanation:

The variable X is defined as, X = number of defective items in the sample.

In a sample of 20 items there are 4 defective items.

The probability of selecting a defective item is:

`P (X)=(4)/(20)=0.20`

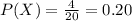
A random sample of n = 3 items are selected at random.

The random variable X follows a Binomial distribution with parameters n = 3 and p = 0.20.

The variance of a Binomial distribution is:

`V(X)=np(1-p)`

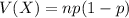
Compute the variance of X as follows:

`V(X)=np(1-p)=3*0.20*(1-0.20)=0.48`

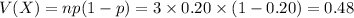
Compute the standard deviation (σ (X)) as follows:

`\sigma (X)=√(V(X))=√(0.48)=0.693`

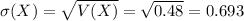
Thus, the variance and standard deviation of X are 0.48 and 0.693 respectively.

Now compute the variance of (20 - X) as follows:

`V(20-X)=V(20)+V(X)-2Cov(20,X)=0+0.48-0=0.48`

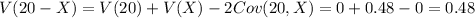
Compute the standard deviation of (20 - X) as follows:

`\sigma (20-X)=√(V(20-X)) =√(0.48)0.693`

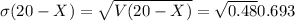
Thus, the variance and standard deviation of (20 - X) are 0.48 and 0.693 respectively.