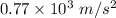Answer:
The average acceleration of the bearings is
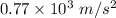
Step-by-step explanation:
Given that,
Height = 1.94 m
Bounced height = 1.48 m
Time interval
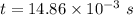
Velocity of the ball bearing just before hitting the steel plate
We need to calculate the velocity
Using conservation of energy

Put the value into the formula
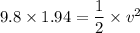

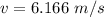
Negative as it is directed downwards
After bounce back,
We need to calculate the velocity
Using conservation of energy
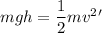
Put the value into the formula
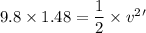
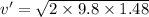
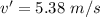
We need to calculate the average acceleration of the bearings while they are in contact with the plate
Using formula of acceleration
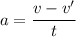
Put the value into the formula
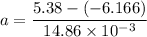
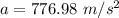
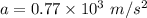
Hence,The average acceleration of the bearings is