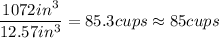Question

1.John has a sink that is shaped like a half-sphere. The sink has a volume of 1072 in. One day, his sink

clogged. He has to use one of two cylindrical cups to scoop the water out of the sink. The sink is completely
full when Anthony begins scooping
(a) One cup has a diameter of 2 in, and a height of 4 in. How many cups of water must Anthony scoop
out of the sink with this cup to empty it? Round the number of scoops to the nearest whole number
***Find the volume of the cup. Divide the volume of the sink by the volume of the cup***
Answer:

Answer 1

`\large\boxed{\large\boxed{85cups}}`

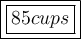
Step-by-step explanation:

1. Volume of a cup

The shape of the cup is a cylinder. The volume of a cylinder is:

`\text{Volume of a cylinder}=\pi * (radius)^2* height`

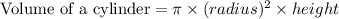
The diameter fo the cup is half the diameter: 2in/2 = 1in.

Substitute radius = 1 in, and height = 4 in in the formula for the volume of a cylinder:

`\text{Volume of the cup}=\pi * (1in)^2* 4in\approx 12.57in^3`

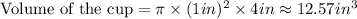
2. Volume of the sink:

The volume of the sink is 1072in³ (note the units is in³ and not in).

3. Divide the volume of the sink by the volume of the cup.

This gives the number of cups that contain a volume equal to the volume of the sink:

`(1072in^3)/(12.57in^3)=85.3cups\approx 85cups`