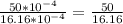Question

For a three-stage cascaded filter (where the output impedance of each stage is negligible compared to the input impedance of the next stage), the gains of the three stages at different frequencies are

Answer 1

The answer is 4.905 dB

Step-by-step explanation:

Let say that that signal is sinusoidal i.e Am sin(wt)

Hence the power of the signal
`=(Am^2)/(2)`

From the question we are given that Amplitude Am = 10mV

substituting this value into the power formula

Power of the signal
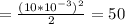`=((10*10^(-3))^(2))/(2)= 50`μW

From the question we where given that the signal to noise ratio is

`((S)/(N))_dB = 5dB`

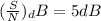
Note: The dB of a value means the same thing as 10 log of the value

`10log((S)/(N) ) = 5`

`(S)/(N) = 10^(0.5) =3.16`

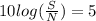
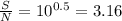
Now to obtain noise power we make it the subject in the above equation

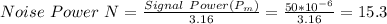`Noise \ Power \ N = (Signal \ Power (P_m))/(3.16) = (50*10^(-6))/(3.16) =15.3`μW

Now to obtain the overall signal gain we multiply the individual gain for the frequency that we are considering i.e 1KHz as our signal

Overall signal gain =
`G_1G_2G_3 = 10^(-6)*10^(-4)*1 = 10^2`

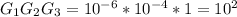
Now that we have gotten this we can now compute the output signal power gain denoted by
`S_o`

`S_o = P_m *(G_1G_2G_3)`

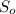
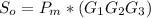
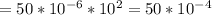`= 50*10^(-6) *10^2 = 50*10^(-4)`W

Now to obtain the overall signal gain we multiply the individual gain for the frequency that we are considering i.e 10KHz as our noise

`N_o = N *(G_4G_5G_6) = 15.3*10^(-6) * 10 * 10^(0.01) * 10 = 16.12*10^(-4)W`

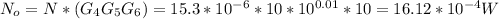
Output signal to noise ratio (S/N) =
`(50*10^(-4))/(16.16*10^(-4)) =(50)/(16.16)`

`((S)/(N)) _dB = 10log((50)/(16.6) ) = 4.905dB`