Answer:
Length of the curve = 1.207 units
Explanation:
y =
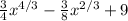 for 1 ≤x≤8
for 1 ≤x≤8
The formula for finding the length of a curve is:
Length of a curve =
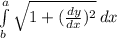
To compute the length we need (dy/dx)². So,
dy/dx =

dy/dx =
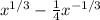
(dy/dx)² = (
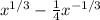 )²
)²
(dy/dx)² =
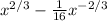
Length of a curve =
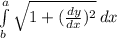
=
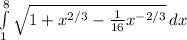
=
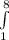 [(1 + x^(2/3) - (1/16)(x^-2/3)]^1/2 dx
[(1 + x^(2/3) - (1/16)(x^-2/3)]^1/2 dx
= 2/3 [(1 + x^(2/3) - (1/16)(x^-2/3)]^3/2 * [(2/3)*x^-1/3 + (1/24)*x^(-5/3)]
Applying limits 1 to 8:
(2/3)*[(1 + (8)^(2/3) - (1/16)(8)^(-2/3)]^3/2 * [(2/3)*(8)^(-1/3) + (1/24)*(8)^(-5/3)] - (2/3)*[(1 + (1)^(2/3) - (1/16)(1)^(-2/3)]^3/2 * [(2/3)*(1)^(-1/3) + (1/24)*(1)^(-5/3)]
= (2/3)*(11.12)*(0.3346) - (2/3)*(2.6968)*(0.7083)
= 2.4805 - 1.2734
Length of the curve = 1.207 units