Question

The top of a 10-ft ladder is leaning against a wall, and the base of the ladder is on the ground. If the top of the ladder slides down the wall at a rate of 2 ft/sec, how fast (in ft/sec) is the bottom of the ladder moving along the ground when the bottom of the ladder is 5 ft from the wall?

Answer 1

Ladder is moving away from the wall with the speed of 3.464 ft/s

Explanation:

Consider the figure attached

Given that top of ladder slides down with the speed of 2ft/sec, i.e

`(dh)/(dt)=2fts^(-1)`

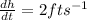
Length of ladder =10 ft

bottom of the ladder is 5 ft from the wall i.e b=5

By pythagorous theorem

`h^2+b^2=100---(1)\\\\h^2=100-(5)^2\\\\h^2=75\\\\h=5√(3)ft`

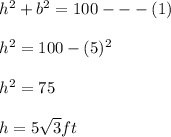
Differentiating equation (1) w.r.to t

`2h(dh)/(dt)+2b(db)/(dt)=\\\\2(5)(db)/(dt)=-2(5√(3))(2)\\\\(db)/(dt)=-2√(3)\\\\(db)/(dt)=-3.464\,ft/s`

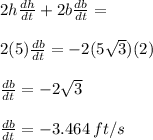
Negative sign shows that ladder is moving away from wall