Answer:
See explanation below.
Explanation:
We assume that the data is given by :
x: 30, 30, 30, 50, 50, 50, 70,70, 70,90,90,90
y: 38, 43, 29, 32, 26, 33, 19, 27, 23, 14, 19, 21.
Where X represent the cost for scholarships in thousands of dollars and y represent the cost of life for an academic semester (The data comes from the web)
We can find the least-squares line appropriate for this data.
For this case we need to calculate the slope with the following formula:
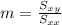
Where:

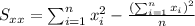
So we can find the sums like this:
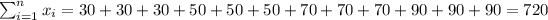
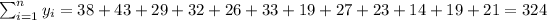
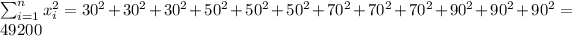
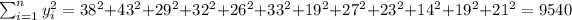
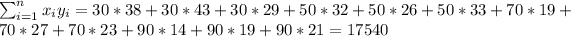
With these we can find the sums:
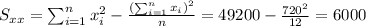
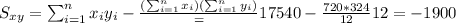
And the slope would be:

Nowe we can find the means for x and y like this:

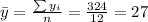
And we can find the intercept using this:
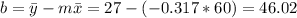
So the line would be given by:
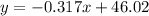
We have an inverse linear relationship since the slope is negative between the variables of interest.