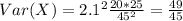Question

A bag contains 5 red and 5 blue balls. Select two at random without replacement. If they are of the same color you win $1.10 otherwise you lose $1. Let X be your winnings. Compute EX and Var(X).

Answer 1

`E(X) = 1.1* (4)/(9) -1*(5)/(9)= -(1)/(15)`

`Var(X) = Var(2.1 I-1) = Var(2.1I) = 2.1^2 Var(I)`

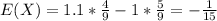
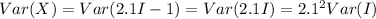
And if we find the variance for the indicator variable we got:

`Var(X)= 2.1^2 (20*25)/(45^2) =(49)/(45)`

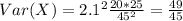
Explanation:

For this case we can define an indicator variable I that is 1 when we win and 0 when we not win.

And we can define the random variable X as the amount of money that we can win like this:

`X = 2.1I-1`

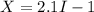
We can find the probability of win like this:

`p_(win)= (5*4)/(10C2)= (20)/(45)= 4/9`

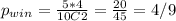
And the probability of no win would be:

`p_(Nowin)= 1-(4)/(9)= (5)/(9)`

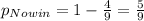
The two possible values for X are 1.1 when we win and -1 when we not win.

The expected value of a random variable X is the n-th moment about zero of a probability density function f(x) if X is continuous, or the weighted average for a discrete probability distribution, if X is discrete.

The variance of a random variable X represent the spread of the possible values of the variable. The variance of X is written as Var(X).

We can find the expected value with this formula:

`E(X) = \sum_(i=1)^n X_i P(X_i)`

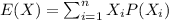
And if we replace the values that we have we got:

`E(X) = 1.1* (4)/(9) -1*(5)/(9)= -(1)/(15)`

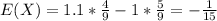
Now in order to find the variance we need to find the second moment defined as:

`E(X^2) = \sum_(i=1)^n X^2_i P(X_i)`

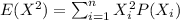
And if we replace we got:

`E(X^2) = (1.1)^2 (4)/(9) - 1^2*(5)/(9) =-(4)/(225)`

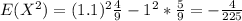
We can calculate the variance using this definition:

`Var(X) = Var(2.1 I-1) = Var(2.1I) = 2.1^2 Var(I)`

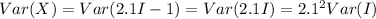
And if we find the variance for the indicator variable we got:

`Var(X)= 2.1^2 (20*25)/(45^2) =(49)/(45)`