Question

A car weighing 10.7 kN and traveling at 13.6 m/s without negative lift attempts to round an unbanked curve with a radius of 64.0 m. (a) What magnitude of the frictional force on the tires is required to keep the car on its circular path? (b) If the coefficient of static friction between the tires and the road is 0.39, is the attempt at taking the curve successful or not ("yes" or "no")?

Answer 1

a) 3156 N

b) Yes

Step-by-step explanation:

a)

When a car moves along a curved road, the frictional force between the tires and the road must provide the required centripetal force in order to keep the car in circular motion.

Therefore, the frictional force must be equal to the centripetal force:

`F_f=m(v^2)/(r)`

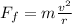
where:

m is the mass of the car

v is the speed of the car

r is the radius of the curve

In this problem, we have:

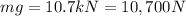`mg=10.7 kN = 10,700 N` is the weight of the car, so the mass of the car is

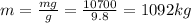`m=(mg)/(g)=(10700)/(9.8)=1092 kg` is the mass

r = 64.0 m is the radius of the curve

v = 13.6 m/s is the speed of the car

Therefore, the magnitude of the frictional force is

`F_f=(1092)(13.6^2)/(64.0)=3156 N`

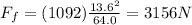
b)

The magnitude of the force of static friction between the tires and the road is given by

`F_f=\mu mg`

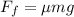
where

`\mu` is the coefficient of friction

m is the mass of the car

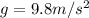`g=9.8 m/s^2` is the acceleration due to gravity

In this problem,

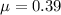`\mu=0.39` is the coefficient of friction

m = 1092 kg is the mass

So the force of friction is

`F_f=(0.39)(1092)(9.8)=4174 N`

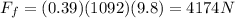
And we see that this force is larger than the centripetal force calculated in part a) and required to keep the car in circular motion: therefore, yes, the coefficient of friction is large enough to keep the car along the curve.