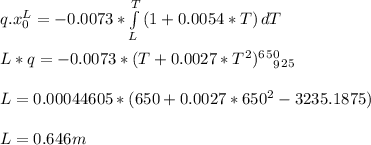Question

It is desired to transport liquid metal through a pipe embedded in a wall at a point where the temperature is 650 K. A 1.2‐m‐thick wall constructed of a material having a thermal conductivity varying with temperature according to k = 0.0073 (1 + 0.0054 T), where T is in K and k is in W/m ⋅ K, has its inside surface maintained at 925 K. The outside surface is exposed to air at 300 K with a convective heat‐transfer coefficient of 23 W/m2 ⋅ K. How far from the hot surface should the pipe be located? What is the heat flux for the wall?

Answer 1

q = 16.366 W/m^2

L = 0.646m

Step-by-step explanation:

Given:

- The inside surface temperature T_i = 925 K

- The pipe surface temperature T_1 = 650 K

- The ambient temperature T_a = 300 K

- The outermost surface temperature = T_rw

- The thermal conductivity coefficient :

- Total thickness of the wall = 1.2 m

k = 0.0073*( 1 + 0.0054*T)

- The convection heat transfer coefficient h = 23 W / m^2K

Find:

How far from the hot surface should the pipe be located? What is the heat flux for the wall?

Solution:

- The conduction through the wall is given by:

`q = -k*(dT)/(dx)\\\\ q.x\limits^1^.^2_0 = - 0.0073*\int\limits^T_L {( 1+ 0.0054*T)} \, dT\\\\ 1.2*q = - 0.0073*(T + 0.0027*T^2)\limits^T^r^w_9_2_5 \\\\q = 0.00608333*(T_r_w + 0.0027*T_r_w^2 - 3235.1875)\\\\q = h*( T_r_w - 300 )\\\\0.00608333*(T_r_w + 0.0027*T_r_w^2 - 3235.1875) = 23*( T_r_w - 300 )`

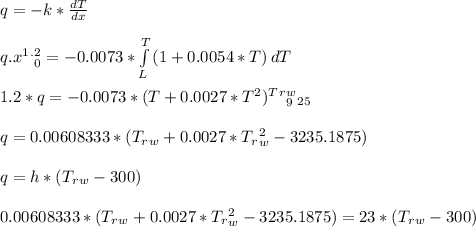
- Solve the above quadratic equation we get:

T_rw = 300.71 K

q = 16.366 W/m^2

- The pipe must be located where the surface temperature of 650 K can be maintained. Hence, we have:

`q.x\limits^L_0 = - 0.0073*\int\limits^T_L {( 1+ 0.0054*T)} \, dT\\\\ L*q = - 0.0073*(T + 0.0027*T^2)\limits^6^5^0_9_2_5 \\\\L = 0.00044605*(650 + 0.0027*650^2 - 3235.1875)\\\\L = 0.646m`