Question

The rate constant of a particular first order reaction is 5.45 x 10^-2 sec^-1 at 40.0 oC. What is the rate constant of this reaction at 65.0 oC if the energy of activation, Ea for this reaction is 65.5 kJ/mol

Answer 1

Answer: The rate constant for the reaction at 65°C is
`0.350s^(-1)`

Step-by-step explanation:

To calculate rate constant at 65°C of the reaction, we use Arrhenius equation, which is:

`\ln((K_(65^oC))/(K_(40^oC)))=(E_a)/(R)[(1)/(T_1)-(1)/(T_2)]`

where,

`K_(65^oC)` = equilibrium constant at 65°C = ?

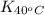`K_(40^oC)` = equilibrium constant at 40°C =
`5.45* 10^(-2)s^(-1)`

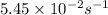
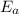`E_a` = Activation energy of the reaction = 65.5 kJ/mol = 65500 J/mol (Conversion factor: 1 kJ = 1000 J)

R = Gas constant = 8.314 J/mol K

`T_1` = initial temperature =
`40^oC=[40+273]K=313K`

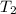`T_2` = final temperature =
`65^oC=[65+273]K=338K`

Putting values in above equation, we get:

`\ln((K_(65^oC))/(5.45* 10^(-2)))=(65500J/mol)/(8.314J/mol.K)[(1)/(313)-(1)/(338)]\\\\K_(65^oC)=0.350s^(-1)`

Hence, the rate constant for the reaction at 65°C is
`0.350s^(-1)`