Option C:
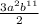 is equivalent to the given expression.
is equivalent to the given expression.
Solution:
Given expression:
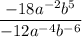
To find which expression is equivalent to the given expression.
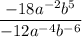
Using exponent rule:

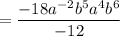

Using exponent rule:
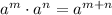
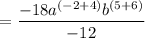
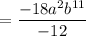
Divide both numerator and denominator by the common factor –6.
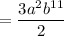
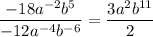
Therefore,
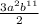 is equivalent to the given expression.
is equivalent to the given expression.
Hence Option C is the correct answer.