Question

For methyl chloride at 100°C the second and third virial coefficients are: B = −242.5 cm 3 ·mol −1 C = 25,200 cm 6 ·mol −2 Calculate the work of mechanically reversible, isothermal compression of 1 mol of methyl chloride from 1 bar to 55 bar at 100°C. Base calculations on the following forms of the virial equation: (a) Z = 1 + B __ V + C ___ V 2 (b) Z = 1 + B′P + C′ P 2 where B′ = B ___ RT and C′= C − B 2 _____ ( RT ) 2 Why don’t both equations give exactly the same result?

Answer 1

a)W=12.62 kJ/mol

b)W=12.59 kJ/mol

Step-by-step explanation:

At T = 100 °C the second and third virial coefficients are

B = -242.5 cm^3 mol^-1

C = 25200 cm^6 mo1^-2

Now according isothermal work of one mole methyl gas is

W=-
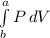
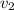
`\int\limits^a_b {P} \, dV`

a=
`v_2\\`

b=
`v_1`

from virial equation

`(PV)/(RT)=z=1+(B)/(V)+(C)/(V^2)\\ \\P=RT(1+(B)/(V) +(C)/(V^2))(1)/(V)\\`

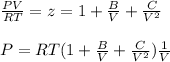
And

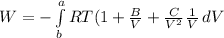
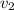
`W=-\int\limits^a_b {RT(1+(B)/(V) +(C)/(V^2)(1)/(V) } \, dV`

a=
`v_2\\`

b=
`v_1`

Now calculate V1 and V2 at given condition

`(P1V1)/(RT) = 1+(B)/(v_1) +(C)/(v_1^2)`

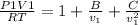
Substitute given values
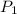`P_1\\` = 1 x 10^5 , T = 373.15 and given values of coefficients we get

`10^5(v_1)/8.314*373.15=1-242.5/v_1+25200/v_1^2`

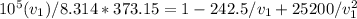
Solve for V1 by iterative or alternative cubic equation solver we get

`v_1=30780 cm^3/mol`

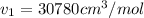
Similarly solve for state 2 at P2 = 50 bar we get

`v_1=241.33 cm^3/mol`

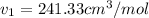
Now

`W=-\int\limits^a_b {RT(1+(B)/(V) +(C)/(V^2)(1)/(V) } \, dV`

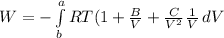
a=241.33

b=30780

After performing integration we get work done on the system is

W=12.62 kJ/mol

(b) for Z = 1 + B' P +C' P^2 = PV/RT by performing differential we get

dV=RT(-1/p^2+0+C')dP

Hence work done on the system is

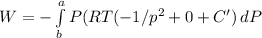
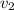
`W=-\int\limits^a_b {P(RT(-1/p^2+0+C')} \, dP`

a=
`v_2\\`

b=
`v_1`

by substituting given limit and P = 1 bar , P2 = 50 bar and T = 373 K we get work

W=12.59 kJ/mol

The work by differ between a and b because the conversion of constant of virial coefficients are valid only for infinite series