Answer:
The answers to the question are
Magnitude = 4/9·q
Sign = Opposite in sign to those of q and 4·q, that is, -ve where q and 4·q are +ve
x coordinate L/3
or
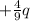 at x coordinate =
at x coordinate =
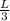
Explanation:
To solve the question, we note that
Force between charges is given by
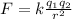 , therefore the force between the two charges q and 4q is
, therefore the force between the two charges q and 4q is
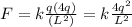
For equilibrium, the charge on the third charge p, will be opposite to those of q and 4·q and the location will be between 0 and L
Therefore the force between the p and q placed at a distance d from q =
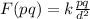 and the force between p and 4q =
and the force between p and 4q =
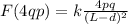
For equilibrium, these two forces should be equal, therefore
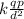 =
=
 which gives
which gives
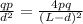 and by cross multiplying, we have
and by cross multiplying, we have
(L-d)²× p×q = d²× 4×p×q → (L-d)² = d²× 4 = (L-d)² - d²× 4 = 0 or
L² - 2·d·L -3·d² = 0, which could be factored as
(L+d)×(L-3·d) = 0 Which gives either L = -d or L = 3·d
Since L > d as d is in between 0 and L, then the correct solution is L = 3·d
Since the system is in equilibrium then
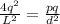 or
or
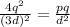
Cancelling like terms gives

Therefore the magnitude of p = 4/9·q
The location of p is L/3 from the charge q