Answer:
The 5 hour growth/decay factor for the number of milli-grams of caffeine in Alan's body is 0.4759
Explanation:
We are given the following in the question:
Caffeine in Alan's body decreases exponentially.
10 hour delay factor = 0.2265
We have to calculate 5 hour delay factor of Alan's body.
Let b be 1 hour delay factor.
Then, we can write
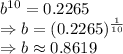
To calculate 5-hour growth/decay factor:
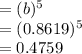
Thus, the 5 hour growth/decay factor for the number of milli-grams of caffeine in Alan's body is 0.4759